パパ塾【数学Ａ場合の数】円順列・重複順列　イメージで公式を作る教え方を伝授！

前回、順列という便利な考え方を学習しました。

【前回記事】

パパ塾【数学Ａ場合の数】順列の教え方基本から応用まで一気に可能！

n 個の中から r 個を取り出して、
並べる並べ方、
それが順列でした。

さらにその応用問題も扱いました。

ポイントとしては、
条件のあるところから考えること。

条件のある部分に何通りの入り方があって、
残りの部分がどうなるのかを考察
積の法則で答えを出す
というものでした。

今回は、それをちょっと違う方向にアレンジしたもの
円順列と重複順列について扱います。

円順列とは文字通り、円形に並べた時の総数。

重複順列とは、
同じ文字や数を繰り返し使ってもいい時の順列

ちょっと考え方が異なります。

それぞれの場合について、
公式と成り立つ意味合いを、
考えていきましょう。

この２つは、仕組みが分かれば、
公式を導き出すことも
簡単にできることと思います。

緑色背景２本が親子のやり取りを楽しむフルバージョン
ピンク色背景が、教えることに特化した、解説バージョンです。

なお、長丁場の動画となりますので、
視聴速度を1.25倍～1.5倍にすると、
効率よく学習できるのではと思います。

ご意見等ございましたら、コメント欄からぜひお寄せください。

また、チャンネル登録、高評価をいただけますと幸いです。

この記事の最後には、
授業ノートも掲載しています。

それでは内容に入っていきましょう。

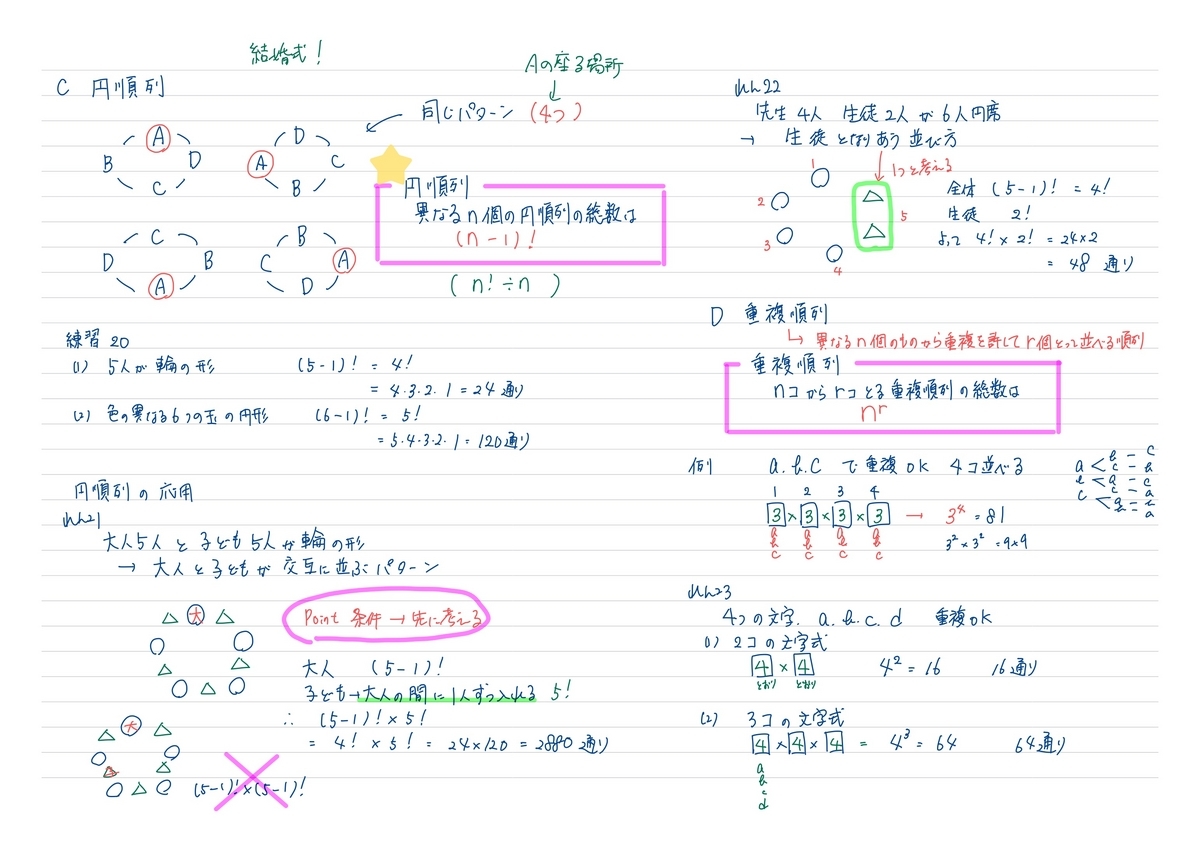
まずは円順列について。

円順列は、円形に並べた時の並べ方の総数で、

例えば４人で中華料理などで円卓を囲む時、
右、正面、左に同じ人が座るパターン
同じものが４通りできますよね。

ですので、通常の順列の「４！」を同じパターンの
４で割り算したものが、円順列の総数になります。

この基本的な仕組みが分かることがまずは大切。

これで、何人が円形で座ったとしても、
１人を固定をすると、
割り算が見えてくるので、
ぐっと考えやすくなりますね。

さて、この円順列、
実は考え方が難しい部分があります。

それは、条件が入ったとき。

・特定の２人や３人が隣り合うとき
・正面に来る人が決まるとき
・男女が交互に並ぶとき

最後に積の法則でかけ算をするということに気づく人は
多いかもしれませんが、
そのかける数（条件外）を間違えてしまうことが、
実は多いのです。

詳しくは１問１問問題が出るごとに解説をして
考えていく必要があります。

この手の問題に出会ったときは、ちょっと立ち止まって
状況をよく見る必要があります。

重複順列は
公式そのものを自分で作ることも可能です。

亀きちとしては、
自分で公式を作ることをお勧めしたいです。

箱を用意して、
その箱の中に何通りの文字や数が入るか
それを積の法則で掛け合わせる

それで公式ができ上がるわけですので。

積の法則の応用版という形で、
理解してもらえればなと思っています。

もちろん、条件が入ることもありますが、
条件を先に考えることにより、
ひょひょいとクリアできます。

割と捉えやすい分野だと思います。

それでは、授業ノートです！

亀きちのブログが、電子書籍に。いつでもどこでも数学を楽しく！第１～４巻絶賛発売中！

公式LINE開設！
旬の情報や、勉強法、授業で使えるプチネタなどタイムリーにお届け！
ご登録お待ちしています！　(^^♪

リアルタイムでブログ記事を受け取りたい方！読者登録はこちらから　　

ご質問・ご感想・ご要望等お気軽にお問い合わせください。

　また、「気になる」「もう一度読み返したい」記事には
↓↓「ブックマーク」もどしどしお願いします